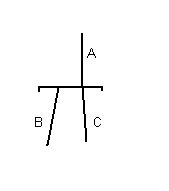Difference between revisions of "OR node"
(new page) |
m |
||
| Line 5: | Line 5: | ||
==== Ordered OR ==== | ==== Ordered OR ==== | ||
| − | Sequential ordering would make no sense for the OR node, since only one of the alternatives occurs at a time. For disjunctions, we have | + | Sequential ordering would make no sense for the OR node, since only one of the alternatives occurs at a time. For disjunctions, we have [[precedence ordering]]: the line shown off to the side of the OR node takes precedence over the other line: If it can be taken, it is. The other line is the ''default line''. The line which takes precedence is drawn off to the side, either the right or the left side, depending only on the practical consideration of which will give the more readable diagram. The typical situation is that the line which takes precedence is immediately connected to the node specifying the conditions under which the line can be taken. The other line, connected at the center of the node, is the default line, taken if the conditions for the precedence line are not present. |
==== OR Node Activation ==== | ==== OR Node Activation ==== | ||
'''Downward Ordered OR''': | '''Downward Ordered OR''': | ||
| − | [[Image:DOO. | + | |
| + | [[Image:DOO.gif]] | ||
| + | |||
Downward activation from A goes to B if possible, otherwise to C. Upward activation from B ''or'' C goes to A. | Downward activation from A goes to B if possible, otherwise to C. Upward activation from B ''or'' C goes to A. | ||
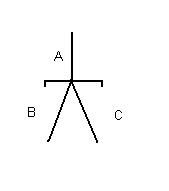
'''Downward Unordered OR''': | '''Downward Unordered OR''': | ||
| + | |||
[[Image:DUO.jpg]] | [[Image:DUO.jpg]] | ||
| + | |||
Downward activation from A goes to b ''and'' [sic] C. Upward activation from B ''or'' C goes to A. | Downward activation from A goes to b ''and'' [sic] C. Upward activation from B ''or'' C goes to A. | ||
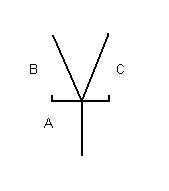
'''Upward Unordered OR''': | '''Upward Unordered OR''': | ||
| + | |||
[[Image:UUO.jpg]] | [[Image:UUO.jpg]] | ||
| + | |||
Upward activation from A goes to B ''and'' C. Downward activation from B ''or'' C goes to A. | Upward activation from A goes to B ''and'' C. Downward activation from B ''or'' C goes to A. | ||
Revision as of 02:50, 6 October 2008
An OR node is a node in compact relational network notation. It looks like a single square bracket turned on its side and pointing upward or downward. To one side, either the upward or the downward, is connected one line; this is the singular side of the node. To the other side are connected two or more lines; this is the plural side of the node. The lines on the plural side are shown, by their connections to the OR node, to be in a disjunctive relationship. The OR node thus shows a relationship of alternation as opposed to combination, which is shown by the AND node.
Like the AND node, the OR node has two general types, the ordered and the unordered:
Ordered OR
Sequential ordering would make no sense for the OR node, since only one of the alternatives occurs at a time. For disjunctions, we have precedence ordering: the line shown off to the side of the OR node takes precedence over the other line: If it can be taken, it is. The other line is the default line. The line which takes precedence is drawn off to the side, either the right or the left side, depending only on the practical consideration of which will give the more readable diagram. The typical situation is that the line which takes precedence is immediately connected to the node specifying the conditions under which the line can be taken. The other line, connected at the center of the node, is the default line, taken if the conditions for the precedence line are not present.
OR Node Activation
Downward Ordered OR:
Downward activation from A goes to B if possible, otherwise to C. Upward activation from B or C goes to A.
Downward Unordered OR:
Downward activation from A goes to b and [sic] C. Upward activation from B or C goes to A.
Upward Unordered OR:
Upward activation from A goes to B and C. Downward activation from B or C goes to A.
Sources
- LangBrain.
- Lamb, Sydney M., Pathways of the Brain: The Neurocognitive Basis of Language, John Benjamins, 1999.